

The Wu Bei Yao Lue is part of the flood of Ming military writing which followed the suppression of the Japanese Pirates along South and Eastern Chinese coast under the leadership of Yu Da-you and Qi Ji-guang in the 1580s.
The book was considered of sufficient strategic importance that it was banned under the literary inquisition of the Qing Emperor Qian Long.
That said, in terms of technique, later critics such as Gao Ying did not regard it highly. The style of archery still displayed some of the tendency towards showiness rather than simple practicality.
Despite such criticisms the book is beautifully illustrated with woodblock prints. So regardless of what later commentators thought of the form portrayed, it remains a valuable resource for allowing the reader to see directly what effect the textual explanations were seeking to achieve.
An interesting point to note is that the body position illustrated he is clearly the same as the one which can be seen in the painting from the Historiographical institute in Tokyo which is reproduced on page 210-211 of the ‘Cambridge Illustrated History of China’ by Patricia Buckley Ebrey (ISBN 0-521-43519-6).
Note also that the bow being used is quite different from the heavy Manchu bows that you can see in photographs from the nineteenth century. They bear a closer resemblance to the traditional bows now in use in Korea.
Stephen Selby
October 1998
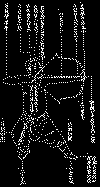
(Click on the picture to bring up a full-page version)
This picture illustrates a military and civil examination standard position which was popular in the Ming and Qing Dynasties. The stiff extension of the forward leg was a fashion of the time, and was criticised by some contemporary and later writers. In Chinese archery, there is always a basic presumption of right-handedness: but the ability to shoot with either hand was regarded as a special level of skill. The Chinese labels (to which I have added reference numbers) read as follows:
| 1 | Elbow tightly bent |
| 2 | String close in to the right cheek |
| 3 | Right pupil at the inner corner of the eye |
| 4 | Left pupil at the outer corner of the eye |
| 5 | The armpit, inside of the elbow and web of the thumb (called the ‘three cavities’) all held level. |
| 6 | Elbow joint aligned vertically (inside of elbow facing up) |
| 7 | Wrist straight with the force taken between forefinger and thumb. |
| 8 | Thumb pressed against the middle finger and level with it. |
| 9 | The point of the forefinger should hang down and not extend too far beyond the thumb |
| 10 | The space between forefinger and thumb must be held tense |
| 11 | Full draw is reached when the point of the arrow reaches the end of the middle finger. |
| 12 | Back leg bowed |
| 13 | Right leg as if lightly stepping on something |
| 14 | Almost in a ‘V’ position |
| 15 | Slightly off the line to the target |
| 16 | Left toe pointing slightly to the right making the ankle extend slightly forward. |
Up-dated 12 October